
Vedic Sutras
1. Ekadhiken Purven (एकाधिकेन पूर्वेण):
Increasing (एकाधिक) a number to the digit which comes before (पूर्व)
For example, Edadhik of 12
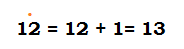
It is represented by a dot on the number which has to be increased.
2. Ek Nyunen Purven (एक न्यूनेन पूर्वेण):
Decreasing (एक न्यूनेन) a number to the digit which comes before (पूर्व)
Put a dot (nyun) below the unit place of the number to find ek nyunen of that number.
For example, ek nyunen of 57 = 57-1 = 56
3. Vinculum (विनकूलम) Number:
Negative numbers are called VInculum and are represented by a bar on the number.
e.g. 2 (called Vinculum 2)= -2
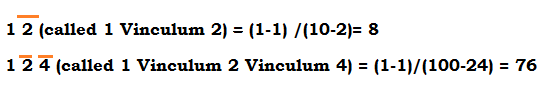
| Questions from CGPSC Mains Examinations |
| 2015 What is Vinculum Number? (10 Marks) i. Convert general number 289 into vinculum number. ii. Convert vinculum number 1 |
4. Aadhar (Base), Upadhar (Sub-base) and Vichalan (Deviation):
For simplifying calculations 10 aur multiples of 10 is often taken as Adhar (Base).
Upadhar (Sub-base) is a multiple of Base. For example, if Base is 10, 10x is a Sub-base.
Vichalan (Deviation) is deviation from the Base.
Vichalan (Deviation) = Number – Base
5. Nikhilam – navatah charanam dashatah (निखिलम– नवतः चरणम दशतः):
In ancient Indian mathematician, number 9 was called as Param or Brahma Number (परम या ब्रह्मा अंक) and number 10 was called as Purn Number (पूर्ण अंक).
Nikhilam means- Charam (unit digit) from 10 and others from 9
For example; it can be used for converting a number in to its Vinculum Number.
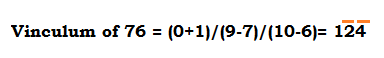
| Steps |
| 1. Subtract the unit digit from 10, put rekhank on the number. 2. Subtract other digits from 9, put rekhank on every number. 3. Put ekadhik on the last number if it is 0 or lesser than 5. |
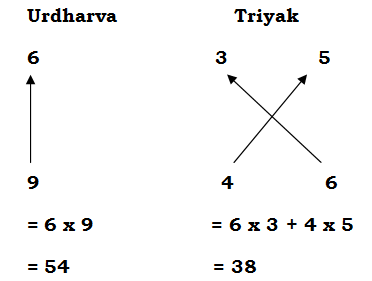
6. Urdharva Triyagyabhyam (उर्ध्व तिर्यग्भयाम):
Urdharva: Above or straight (ऊपर या सीधा)
Tiryak: Cross (तिरछा)
7. Paravartya Yojyet (परावर्त्य योजयेत):
Paravartya Yojyet means use after changing signs.
(+) becomes (-), (-) becomes (+), (x) becomes (÷) and (÷) becomes (x)
Addition
1. Ekadhiken Purven (एकाधिकेन पूर्वेण)
Let’s take an example, 549 + 234 + 403
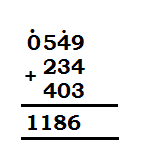
| Steps: |
| 1. Starting from first column; 3+4+9=16, write 6 in the units place and put a dot (ekadhik) on second column (i.e. 4). 2. One dot is treated as 1, add second column digits; 0+3+4+1=8, write 8 in tens place. 3. 4+2+5= 11, write 1 in thousands place and put a dot on fourth column. |
Subtraction
1. Ekadhiken Purven (एकाधिकेन पूर्वेण):
Find 34 – 18
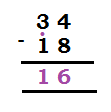
| Steps: |
| 1. Since 8>4, put a dot on 1 (ekadhik). 2. Purak of 8= 10-8=2 is added to 4; 4+2=6 3. One dot makes it 1+1=2, subtract it from 3; 3-2=1 |
2. Ek Nyunen Purven (एक न्यूनेन पूर्वेण):
Find 560-374

| Steps: |
| 1. It is same as that of Ekadhiken Purven but instead of ekadhi, a nyun sign is put below the digit. 2. First column, 0+6 (purak of 4). Put a nyun sign on 6. 3. Second column, 5 (nyun of 6)+ 3 (purak of 7)= 8. Put a nyun sign on 5. 4. Third column, 4 (nyun of 5) – 3=1 |
Addition and Subtraction (Mixed)
Let’s take an example: 423-654+847-126+204
Our example may be represented as (using Vinculum)
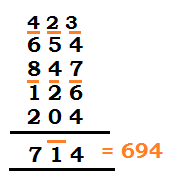
| Steps: |
| 1. Starting from the units place: 3 + 2. Tens place: 2 + 3. Hundreds place: 4 + 4. Final answer is 7 5. It can be converted into a simple number by the following method: |
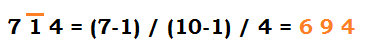
- Rekhank digit can be subtracted from 10 which affect the digit left to it.
1will become (10-1)= 9- 7 will become (7-1)= 6
- Therefore final answer is 6/9/4= 694
| Questions from CGPSC Mains Examinations |
| 2014 Simplify using Vedic method: (08 Marks) 784 + 511 – 287 – 186 + 432 – 279 |
Multiplication
1. Ekadhiken Purven (एकाधिकेन पूर्वेण):
Multiplication of two numbers by this method is quite easy when the sum of their Charam Numbers (Units Digits) is 10 or powers of 10.
Let’s take an example: 95 x 95 (Charam Numbers 5+5=10)
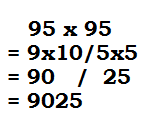
| Steps: |
| 1. There are two parts in the product- left and right parts. 2. The product of Charam numbers will come in the right part. i.e. 5 x 5 =25 (right part will have 2 digits as sum of charam number has only one 0) 3. The product of other Nikhilam number and its ekadhi will come in the left part. i.e.9 x 10= 90 |
Let’s take another example, 586 x 514 (86+14=100)
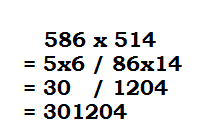
| Steps: |
| 1. There are two parts in the product- left and right parts. 2. The product of Charam numbers will come in the right part. i.e. 86 x 14 =1204 (right part will have 4 digits as sum of charam number has two 0s) 3. The product of other Nikhilam number and its ekadhi will come in the left part. i.e.5 x 6= 30 |
| Questions from CGPSC Mains Examinations |
| 2013 Use Vedic mathematics to solve the following: i. The product of 2104 and 3072 ii. The square of 201 (04 Marks) |
2. Ek Nyunen Purven (एक न्यूनेन पूर्वेण):
Take an example, 8 x 9
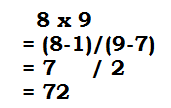
| Steps: |
| 1. There are two parts in the product- left and right parts. 2. Left part= first number-1= 8-1=7 3. Right part= second number- left part= 9-7=2 4. Hence 8 x 9 = 72 |
Take another example, 68 x 999
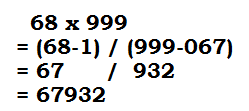
3. Nikhilam – aadhar(निखिलम–आधार):
Let’s take an example, 12 x 14 (Base=10)
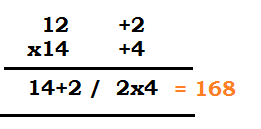
| Steps: |
| 1. There are two parts in the product- left and right parts. 2. Write deviations from the base in front of the numbers. 12-10=2 and 14-10=4 3. The product of the deviations will come in the right part. 2×4=8 (right part will have 1 digit as the number of 0 in the Base) 4. The sum of a number and deviation of another number will come in left part. i.e. 14+2=16 or 12+4= 16. |
Let’s take another example, 92 x 87 (Base=100)
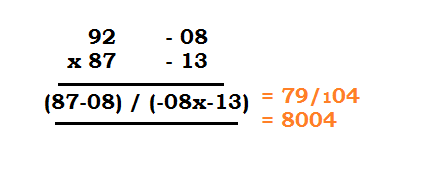
There will be only 2 digits in the right part (as Base=100), therefore the product 104 is taken as 04 and 1 is carried over to the left part.
Division
1. Nikhilam – aadhar(निखिलम–आधार):
Take an example: 311÷8 (Base=10)
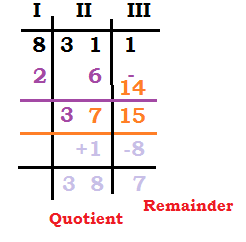
| Steps: |
| 1. Divide the dividend in three parts- divisor (I), digits equal to number of 0s in the base (III) and remaining digits (II) 2. Write the purak (10-8=2) in part I. 3. Draw a line as shown, below the line write down the first digit (i.e.3) and multiply the purak with 3 (i.e. 6) in the second row. Add the numbers (i.e. 1+6=7). 4. In III column second row, nothing will come. In the third row, product of purak and 7 (i.e. 14) will come. 5. II part= Quotient=37, III part= Remainder=15 6. Since Remainder > Divisor, extend the rows. Subtract it with the divisor and +1 in the II part. 7. Add the numbers again. |
Take another example, 10025 ÷88
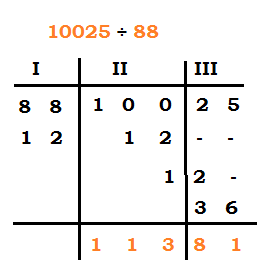
| Steps: |
| 1. Divide the dividend in three parts- divisor (I), digits equal to number of 0s in the base (III) and remaining digits (II) 2. Write the purak (100-88=12) in part I. 3. Draw a line as shown, below the line write down the first digit (i.e.1) and multiply the purak with 1 (i.e. 12) in the second row. Add the numbers (i.e. 0+1=1). 4. In III column second row, nothing will come. In the third row, product of purak and 1 (i.e. 12) will come with 1 in part II and 2 in part III. 5. In the fourth row part III, the product of 3 x 12= 36 will come. 6. Add column wise. 7. II part= Quotient=1123, III part= Remainder=81 |
2. Urdharva Triyagyabhyam (उर्ध्व तिर्यग्भयाम):
Take an example, 23754 ÷74

| Steps: |
| 1. Divide the dividend in three parts- divisor written in two rows (I), 4 is called the Dhwajank; digits equal to number of 0s in the base (III) and remaining digits (II). 2. In part II, 23 ÷7 = 3, remainder= 2. Write the quotient below the horizontal bar and remainder inside the bar below the space between 3 and 7. 3. New dividend= 27 and the corrected dividend= 27- quotient x dhwajank (3 x 4)= 15. 4. 15 ÷ 7 = 2, remainder=1. 5. New dividend= 15, corrected dividend= 15- 2 x 4 = 7, remainder=0 6. Hence, Quotient= 321 and Remainder=0 |
3. Paravartya Yojyet (परावर्त्य योजयेत):
Take an example, 1358 ÷ 113 (Base=100)
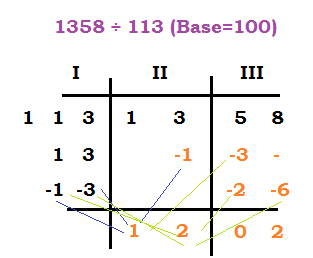
| Steps: |
| 1. Divide the dividend in three parts- divisor (I), digits equal to number of 0s in the base (III) and remaining digits (II). 2. In part I, deviation of the divisor= 113-100=13 and its Paravartya (changed sign)= -1 -3 3. Draw a line as shown, below the line write down the first digit (i.e.1) and multiply the first digit of Paravartya with 1 (i.e. -1) which will come in the second row. Add the numbers (i.e. 3-1=2). 4. In III column second row, the product of the second digit of Paravartya with 1 (i.e. -3) will come in the second row. 5. In the fourth row part III, the product of -1 x 2= -2 and -3 x 2=-6 will come. 6. Add column wise. 7. Hence, Quotient= 12 and Remainder= 2 |

 Home
Home Syllabus
Syllabus Contact Us
Contact Us




